Test ANOVA Kruskala-Wallisa
Test ten jest nieparametryczną alternatywą jednoczynnikowej analizy wariancji. Za pomocą tego testu porównujemy rozkłady kilku zmiennych:
(wszystkie próby pochodzą z jednej populacji)
(nie wszystkie próby pochodzą z tych samych populacji).
Test ten, podobnie jak test U Manna-Whitneya, opiera się na rangach obserwacji. Jeśli wszystkie próby pochodzą z jednej populacji, spodziewamy się, że średnie rangi w poszczególnych grupach będą zbliżone. Statystyka testowa wyraża się wzorem:
,
gdzie:
- - suma rang w i-tej grupie,
- - liczebność i-tej grupy,
- - łączna liczebność wszystkich grup.
Jeśli hipoteza zerowa jest prawdziwa, statystyka ta ma rozkład o stopniach swobody (prawostronny obszar krytyczny).
Ze względu na brak konieczności spełnienia kłopotliwego założenia odnośnie normalności rozkładów, Test ANOVA Kruskala-Wallisa, obok testu U Manna-Whitneya, jest prawdopodobnie najpowszechniej stosowanym testem jednorodności rozkładów w różnego rodzaju badaniach, w tym np. badaniach klinicznych z zakresu medycyny, biologii i dziedzin pokrewnych, badaniach socjodemograficznych, badaniach komercyjnych, w tym m.in badaniach marketingowych czy badaniach rynku i opinii oraz wielu innych.
PRZYKŁAD
badanie. W celu porównania 4 metod leczenia pewnego schorzenia pobrano 10-elementowe
próby losowe spośród osób, które podlegały leczeniu odpowiednio metodą I, II, III i IV. Wyniki badania
podano w umownej skali oraz przyporządkowano im odpowiednie rangi.
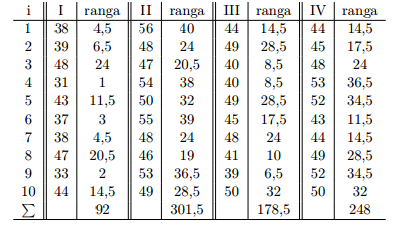
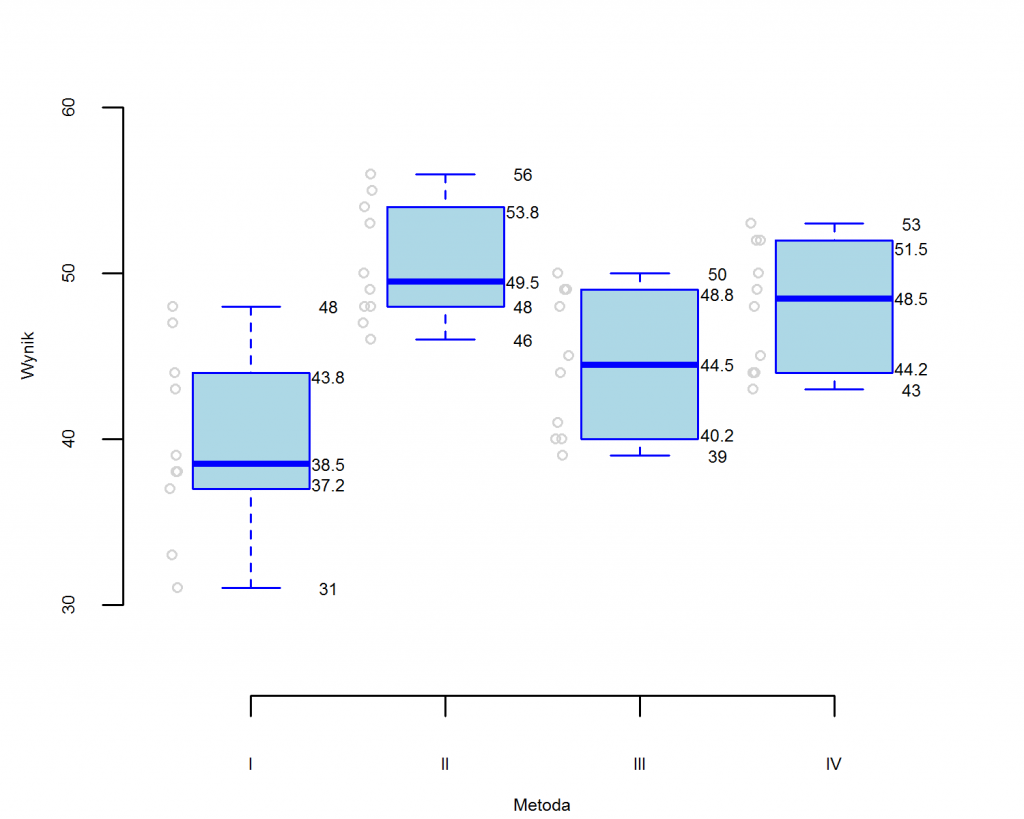
Otrzymane wnioski potwierdza graficzna interpretacja danych na na wykresie pudełkowym:



 Kontakt
Kontakt





 (+48) 666069834
(+48) 666069834
 statystyka@biostat.com.pl
statystyka@biostat.com.pl





