PCA - Założenia oraz kryteria wyboru

Sprawdzanie założeń oraz silnych korelacji między zmiennymi

W przypadku macierzy korelacji do sprawdzania założeń służy tzw. Test Bartletta. Jako hipotezę zerową należy wtedy przyjąć, że macierz korelacji jest równa macierzy jednostkowej. Do oceny adekwatności macierzy korelacji wykorzystujemy współczynnik Kaisera-Mayera-Olkina (KMO). Należy przy tym również zwrócić szczególną uwagę na takie zagadnienia jak: normalność, liczebność próby, punkty odstające, liczbę zmiennych oraz braki danych.

Współczynnik KMO (Kaiser-Meyer-Olkin)

• współczynnik ten porównuje korelacje cząstkowe z dwuzmiennowymi współczynnikami korelacji. Mieści się on w zakresie między 0 a 1. Jeśli przyjmuje wartość 0, przystąpienie do dalszej analizy jest zbędne, gdyż redukcja wymiarowości będzie nieznaczna. Dalsze działania osiągają sensowny efekt dopiero, gdy KMO wynosi przynajmniej 0,5.

Test Sferyczności Bartletta

• test ten zakłada, że macierz współczynników korelacji jest macierzą jednostkową, co oznacza, że nie ma istotnych korelacji między zmiennymi. Odrzucenie hipotezy zerowej jest potwierdzeniem, że analiza redukcji danych przyniesie sensowny rezultat.

Kryteria wyboru

Kryterium wyboru służy do redukcji liczby składowych głównych. Nie istnieje obiektywne kryterium, które jednoznacznie wskazuje na to, które składowe należy usunąć. Do trzech najczęściej stosowanych w praktyce kryteriów zalicza się następujące:

• Skumulowany procent wyjaśnionej wariancji analizowanych zmiennych - Wybieramy najmniejszą liczbę składowych głównych, dla których suma ich wariancji stanowi pewną część wariancji wszystkich zmiennych poddanych redukcji. Ograniczenie dolne jakie suma musi przekroczyć to, według różnych źródeł, 75%, 80% a nawet 90%.
• Kryterium Kaisera - pozostawia się te składowe główne które mają wartości własne większe od jedności (to kryterium jest stosowane, gdy mamy do czynienia z macierzą korelacji). Metoda ta powinna być stosowana gdy ilość zmiennych jest większa od 20. Gdy liczba zmiennych jest mniejsza istnieją szanse wyodrębniania zbyt małej ilości czynników
• Kryterium Cattella - bazujące na analizie wykresu osypiska. Jest to wykres przedstawiający wartości własne pogrupowane niemalejąco. Na wykresie należy odnaleźć tzw. osypisko czynnikowe, czyli ten element wykresu znajdujący się po jego prawej stronie, na którym występuje łagodny spadek wartości własnych. Wartości własne, które znajdują się w osypisku czynnikowym poddajemy redukcji.

PRZYKŁAD - KRYTERIA WYBORU

Kryterium Kaisera (KK) oraz skumulowany procent wyjaśnionej wariancji >80% (SPW):

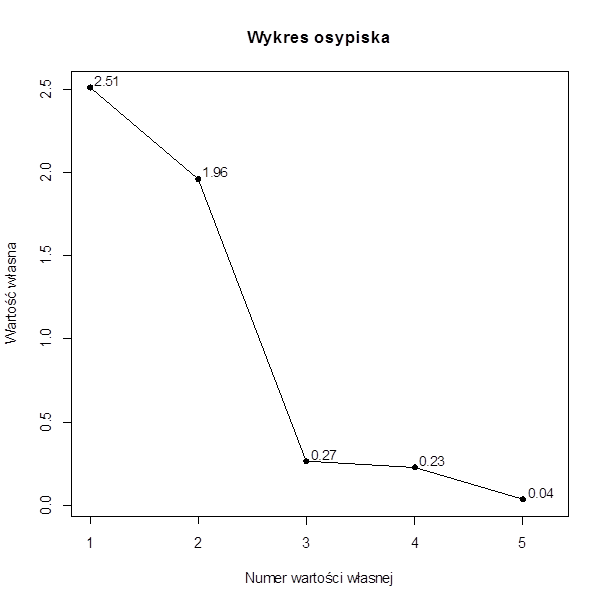
Na powyższym rysunku widać że osypiskiem czynnikowym będą wartości własne o numerach 3, 4 i 5. Zatem pozostawiamy wartości własne znajdujące się na lewo od osypiska tj. te o numerach 1, 2 i ewentualnie 3.