Analiza harmoniczna

Harmoniczna analiza danych ma zgodnie z założeniem prowadzić do utworzenia modelu składającego się z sumy (harmonijek) funkcji kosinusoidalnych lub też sinusoidalnych w określonym przedziale czasowym.
 

        $yt = \alpha_0 + \sum^{\frac{n}{2}}_{t=1} \{\alpha_i \cdot \sin(\frac{2 \cdot \pi}{n} \cdot i \cdot t) + \beta_i \cdot \cos(\frac{2 \cdot \pi}{n} \cdot i \cdot t) \}$

W przypadku występowania tendencji rozwojowej, parametr zostaje zastąpiony funkcją trendu f(t). Zastosowanie klasycznej metody najmniejszych kwadratów sprowadza się do użycia następujących wzorów:

        $a_0 = \frac{1}{n} \cdot \sum^{n}_{t=1} yt$

        $a_i = \frac{2}{n} \cdot \sum^{n}_{t=1} yt \cdot \sin(\frac{2 \cdot \pi}{n} \cdot i \cdot t)$      $i = 1,2,...,\frac{n}{2} -1$

        $b_i = \frac{2}{n} \cdot \sum^{n}_{t=1} yt \cdot \sin(\frac{2 \cdot \pi}{n}\cdot i \cdot t)$    $i = 1,2,...,\frac{n}{2} -1$

dla ostatniej harmoniki $a_\frac{n}{2} = 0$, natomiast $b_\frac{n}{2}$ szacuje się ze wzoru:

        $b_\frac{n}{2} = \frac{1}{n} \cdot \sum^{n}_{i=1} yt \cdot \cos(\pi \cdot t)$

Wielkość amplitud wyznacza się ze wzoru:

        $A_i = \sqrt{a^2_i + b^2_i}$

W celu ich zlokalizowania na osi czasu wyznacza się wartość przesunięcia czasowego$^1$

        $t_t = \frac{\varepsilon_i}{\theta_i}$, gdzie $\theta_i = \frac{2 \cdot \pi}{n} \cdot i$, $\varepsilon_i = arctg \frac{a_i}{b_i}$

W modelu nie trzeba ujmować wszystkich harmonik, wystarczą te, które istotne. W celu stwierdzenia istotności danej harmoniki należy zastosować test Schustera. Nadzieja matematyczna kwadratu amplitudy wynosi:

        $E(A^2_i) = A_n^2 = \frac{4 \cdot \sigma^2}{n}$

gdzie: $\sigma^2$ jest wariancją zmiennej Y, natomiast n jest liczba obserwacji.
Parametr $\sigma^2$ zastępuje się zwykle wariancją z próby.
Schuster udowodnił, że prawdopodobieństwo tego, że $A^2_i$ będzie k razy większe od $A^2_n$ jest równe:
$k = - \ln \alpha$

Przyjmując, że: $k = \frac{A^2_i}{A^2_n}$

Jeśli zajdzie:
$P\{k^* > k\} = \alpha$ to hipotezę Ho głoszącą, że dana amplituda jest statystycznie nieistotna możemy odrzucić na poziomie istotności $\alpha$ i przyjąć, że dana harmonika powinna wejść do modelu$^2$.


$^1$ opracowane na podstawie: M. Cieślak „Prognozowanie gospodarcze – metody i zastosowania” , PWN Warszawa 1997.
$^2$ Mirosław Wójciak skrypt: Zbiór zadań z ekonometrii (w przygotowaniu).

- - -

PRZYKŁAD - prognozowanie sprzedaży usługi teleinformatycznej

Celem niniejszego opracowania jest stworzenie prognozy sprzedaży pewnej usługi proponowanej przez operatora telekomunikacyjnego X na 12 kolejnych miesięcy dysponując obserwacjami miesięcznymi sprzedaży z okresu styczeń 2004 do październik 2005, co daje w sumie 22 obserwacje. Dane, na podstawie których modelowano to zagadnienie to szeregi czasowe czterech obszarów telekomunikacyjnych, które dają w sumie sprzedaż usługi w jednym z regionów kraju. Na ten region składają się obszary oznaczone jako S, T, U oraz W. Wizualna analiza szeregów czasowych czterech regionów pozwoliła na sformułowanie hipotezy, iż każdy region cechuje się różnymi wahaniami o różnej amplitudzie. W związku z tym przeprowadzono analizę cykliczności dla każdego obszaru osobno, sporządzono indywidualne prognozy a następnie zsumowano wyniki otrzymując prognozę dla całego regionu. W kolejnym kroku analizy wyeliminowano ewentualne wahania spowodowane różnicami w ilości dni w poszczególnych miesiącach. Sprowadzono wszystkie miesiące do wykładnika 31 dni. Przeliczenia wykonano wg formuły:

$y_t = \frac{y_t}{c_t} \cdot 31$ Gdzie: $c_t$ - liczba dni miesiąca t; $y_t$ - sprzedaż usługi w miesiącu t w sztukach; Na podstawie posiadanych danych wykonano model metoda wielomianów trygonometrycznych dla okręgu „S”. Wyznaczone wartości poszczególnych parametrów harmonik zamieszczono w tabeli 1 Tabela 1. Parametry modelu dla obszaru S oraz amplitudy harmonik

Kierując się kryterium najwyższego wyjaśniania wariancji do modelu wybrać należy tą harmonikę, która ma najwyższy procent wyjaśniania, czyli harmonikę i=2 oraz harmonikę i=1. Analizując wyniki testu Schustera i przyjmując poziom istotności alfa = 0,05 (czyli k=3), hipotezę głoszącą, iż dana amplituda jest przypadkowa, odrzucić należy tylko w przypadku harmoniki o długości cyklu równym 11 (k*=6,6). Model przyjmuje postać:

        $Y = 27,82 \cdot t + 2374 - 902,917 \cdot \sin(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) - 127,259 \cdot \cos(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) \}$

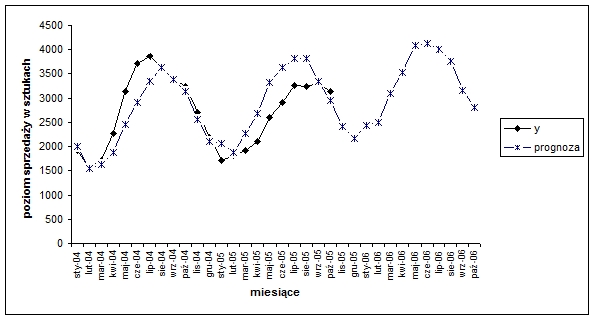
Wartości teoretyczne i prognozy oszacowane na podstawie powyższego modelu po wprowadzeniu korekty ze względu na liczbę dni miesiąca przedstawiono graficznie na wykresie 1.

Wykres 1. Prognozy sprzedaży usługi w okręgu „S” sporządzone na podstawie modelu uwzględniającego harmonikę i=2.

Kolejnym obszarem regionu północnego jest obszar T. oszacowany model dla tego obszaru zaprezentowano w tabeli 2. Tabela 2. Parametry modelu dla obszaru „T”

Kierując się kryterium najwyższego procentu wyjaśniania należy wybrać do modelu harmonikę 2, która wyjaśnia 53% zmienności. Ponadto należy uwzględnić także harmonikę 3 wyjaśniającą 18% zmienności sprzedaży. Te dwie harmoniki tłumaczą w sumie 69% wariancji. Jednakże zgodnie z przyjętym w pracy kryterium testu Schustera do modelu wprowadzono tylko harmonikę i=2. Model ma postać:

        $Y = 23 \cdot t + 3082,2 - 769,65 \cdot \sin(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) - 318,62 \cdot \cos(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) \}$

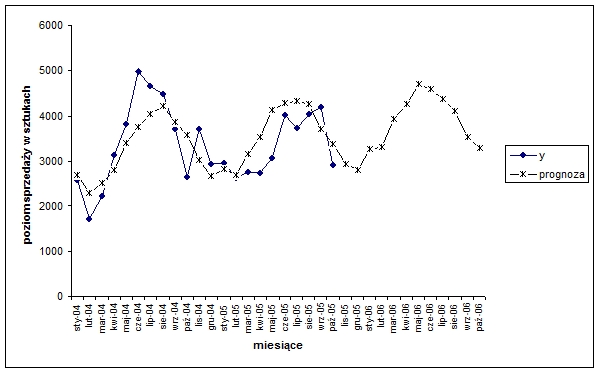
Wartości teoretyczne i prognozy oszacowane na podstawie powyższego modelu po wprowadzeniu korekty ze względu na liczbę dni miesiąca przedstawiono graficznie na wykresie 2.

Wykres 2. Prognozy sprzedaży usługi w okręgu „T” sporządzone na podstawie modelu uwzględniającego harmonikę i=2.

Wyznaczone parametry modelu dla obszaru „U” zawarto w tabeli 3. Tabela 3. Parametry modelu dla obszaru „U”

Największy udział w wyjaśnianiu wariacji ma harmonika i=2 o cyklu 11 miesięcznym. Wyjaśnia ona 51% wahań. Pozostałe harmoniki z uwagi na mały poziom wyjaśniania należy uznać za nieistotne. Model wraz z uwzględnioną funkcją trendu ma postać:

        $Y = 12,63 \cdot t + 1298 - 374,15 \cdot \sin(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) - 110,33 \cdot \cos(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) \}$

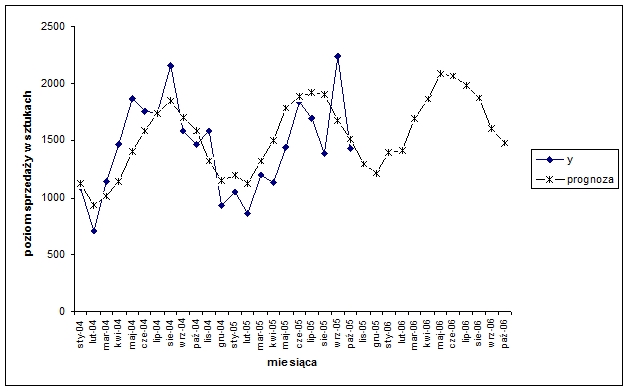
Dopasowanie tego modelu do danych empirycznych (po uwzględnieniu korekty liczby dni w miesiącu) przedstawia wykres 3.

Wykres 3. Prognozy sprzedaży usługi w okręgu „U” sporządzone na podstawie modelu uwzględniającego harmonikę i=2.

Wyniki dla czwartego analizowanego obszaru przedstawiono w tabeli 4. Tabela 4. Parametry modelu dla obszaru „W”

Kierując się kryterium zaproponowanym przez Schustera istotna jest tylko harmonika i=2, dla której k*=6,95. Pozostałe harmoniki na poziomie istotności 0,05 można uznać za nieistotne. Kierując się kryterium wyjaśniania wariancji należy zwrócić uwagę na harmonikę i=8 o długości cyklu 2,8 miesiąca (w przybliżeniu można uznać ten cykl za kwartalny). Wyróżnia się ona znacznie spośród pozostałych i wyjaśnia 8,4% zmienności. Model wraz z trendem ma postać:

        $Y = - 0,07 \cdot t + 2072 - 481,01 \cdot \sin(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) + 320,39 \cdot \cos(\frac{2 \cdot \pi}{22} \cdot 2 \cdot t) \}$

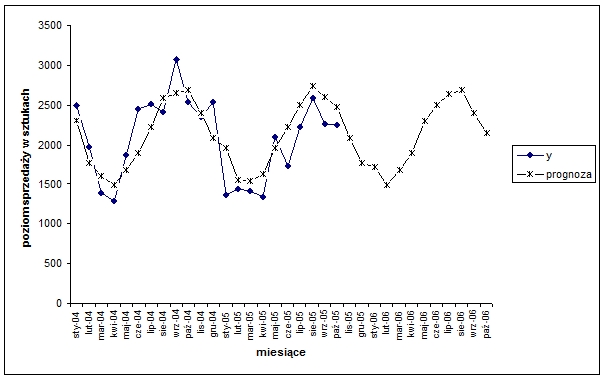
Wartości teoretyczne tak sformułowanego modelu kształtują się następująco.

Wykres 4. Prognozy sprzedaży usługi w okręgu „W” sporządzone na podstawie modelu uwzględniającego harmonikę i=2.

Dysponując prognozami poszczególnych obszarów sformułowano prognozę sprzedaży dla całego regionu będącą sumą prognoz cząstkowych. Taką prognozę przedstawiono w poniższej tabeli.

Wykres 5. Prognozy sprzedaży usługi dla całego obszaru (prognoza na okres listopad 2005 – listopad 2006)

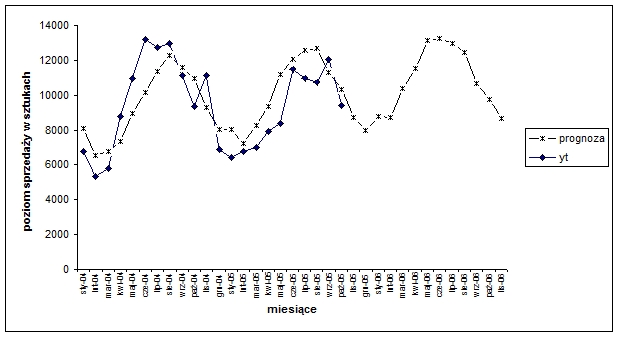
Zgodnie z wynikami zaprezentowanymi na wykresach należy zauważyć, iż zjawisko sprzedaży usługi telekomunikacyjnej cechuje się sezonowością. Sezonowość tą opisano za pomocą metody wielomianów trygonometrycznych, stosując do identyfikacji istotnych cykli test Schustera. Zgodnie z prognozami należy zauważyć, iż sprzedaż osiąga wartości wysokie w miesiącach letnich (lipiec, sierpień) natomiast w miesiącach zimowych sprzedaż jest na zdecydowanie niższym poziomie